Laplacedf
Contents |
Purpose
Laplace distribution.
Synopsis
- prob = laplacedf(function,x,a,b)
Description
Estimates cumulative distribution function (cumulative, cdf), probability density function (density, pdf), quantile (inverse of cdf), or random numbers for a Laplace distribution.
This distribution is a symmetric distribution also known as the double exponential distribution. It is more peaked than the normal distribution Leptokurtic rather than mesokurtic means that it has a sharper peak at the mean in the density plot than a similar normal density
Inputs
- function = [ {'cumulative'} | 'density' | 'quantile' | 'random' ], defines the functionality to be used. Note that the function recognizes the first letter of each string so that the string could be: [ 'c' | 'd' | 'q' | 'r' ].
- x = matrix in which the sample data is stored, in the interval (0,1).
- for function=quantile - matrix with values in the interval (0,1).
- for function=random - vector indicating the size of the random matrix to create.
- a = scale parameter (real and positive).
- b = shape parameter (real and positive).
Note: If inputs (x, a, and b) are not equal in size, the function will attempt to resize all inputs to the largest input using the RESIZE function.
Note: Functions will typically allow input values outside of the acceptable range to be passed but such values will return NaN in the results.
Examples
Cumulative
>> prob = laplacedf('c',0.99,1,2)
prob =
0.4975
>> x = [0:0.1:10];
>> plot(x,laplacedf('c',x,1,2),'b-',x,laplacedf('c',x,3,7),'r-')
Density
>> prob = laplacedf('d',0.99,1,1)
prob =
0.4950
>> x = [0:0.1:10];
>> plot(x,laplacedf('d',x,2,1),'b-',x,laplacedf('d',x,0.5,1),'r-')
Quantile
>> prob = laplacedf('q',0.99,0.5,1)
prob =
4.4120
Random
>> prob = laplacedf('r',[4 1],2,1)
ans =
0.4549
0.4638
0.3426
0.5011
See Also
betadf, cauchydf, chidf, expdf, gammadf, gumbeldf, logisdf, lognormdf, normdf, paretodf, raydf, triangledf, unifdf, weibulldf
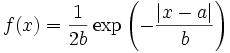
![F(x) = \frac {1} {2} \exp \left [ - \frac {a-x} {b} \right ] \mathrm {I} \left ( x<a \right) +1 - \frac {1} {2} \exp \left [ - \frac {x-a} {b} \right ] \mathrm {I} \left ( x \ge a \right )](math_8c92.png)