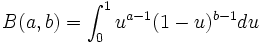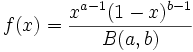Betadf

Betadf

Purpose

Beta distribution.

Synopsis

prob = betadf(function,x,a,b,options)

Description

Estimates cumulative distribution function (cumulative, cdf), probability density function (density, pdf), quantile (inverse of cdf), or random numbers for a Beta distribution.

This distribution is commonly used to model activity time. In its usual form, the data must be in (0,1), but this toolbox will allow both a location and scale parameter (in addition to the a and b above). This may be symmetric or asymmetric.

$B(a,b) = \int_0 ^1 u^{a-1} (1-u)^{b-1} du$

$f(x) = \frac {x^{a-1}(1-x)^{b-1}} {B(a,b)}$

Inputs

• function = [ {'cumulative'} | 'density' | 'quantile' | 'random' ], defines the functionality to be used. Note that the function recognizes the first letter of each string so that the string could be: [ 'c' | 'd' | 'q' | 'r' ].

• x = matrix in which the sample data is stored, in the interval (0,1).

for function=quantile - matrix with values in the interval (0,1).

for function=random - vector indicating the size of the random matrix to create.

• a = scale parameter (real and nonnegative).

• b = shape parameter (real and nonnegative).

Note: If inputs (x, a, and b) are not equal in size, the function will attempt to resize all inputs to the largest input using the RESIZE function.

Note: Functions will typically allow input values outside of the acceptable range to be passed but such values will return NaN in the results.

Options

options is a structure array with the following fields:

• name: 'options', name indicating that this is an options structure,

• scale: {1}, scale for the ordinate, and

• offset: {0}, offset for the ordinate.

The default options structure can be retrieved using: options = betadf('options').

Examples

Cumulative

>> prob = betadf('c', [0.85 0.9],1,2)
prob =
 0.9900
>> x    = [0:0.01:1];
>> plot(x,betadf('c',x,1,2),'b-',x,betadf('c',x,0.5,0.5),'r-')

Density

>> prob = betadf('d', 0.9, 1, 2)
prob =
  0.2000
>> x    = [0:0.01:1];
>> plot(x,betadf('d',x,1,2),'b-',x,betadf('d',x,0.5,0.5),'r-')

Quantile

>> prob = betadf('q',[0.9775 0.9900]',1,2)
prob =
    0.8500
    0.9000

Random

>> prob = betadf('r',[5 1],1,2)
prob =
    0.3791
    0.2549
    0.8169
    0.0216
    0.1516

See Also

cauchydf, chidf, expdf, gammadf, gumbeldf, laplacedf, logisdf, lognormdf, normdf, paretodf, raydf, triangledf, unifdf, weibulldf