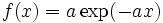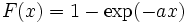Expdf

Expdf

Purpose

Exponential distribution.

Synopsis

prob = expdf(function,x,a)

Description

Estimates cumulative distribution function (cumulative, cdf), probability density function (density, pdf), quantile (inverse of cdf), or random numbers for an Exponential distribution.

The exponential distribution is commonly used to measure lifetime data (time to failure of light bulbs, time to failure of a particular resistor on a circuit board, etc.). It may also measure time between events. The distribution is skewed to the right. The variance is equal to the square of the mean in this distribution. Negative values in the sample are ignored.

$f(x) = a\exp (-ax)$

$F(x) = 1 - \exp(-ax)$

Inputs

• function = [ {'cumulative'} | 'density' | 'quantile' | 'random' ], defines the functionality to be used. Note that the function recognizes the first letter of each string so that the string could be: [ 'c' | 'd' | 'q' | 'r' ].

• x = matrix in which the sample data is stored, in the interval (-inf,inf).

for function=quantile - matrix with values in the interval (0,1).

for function=random - vector indicating the size of the random matrix to create.

• a = mean/scale parameter (real and positive).

Note: If inputs (x, a, and b) are not equal in size, the function will attempt to resize all inputs to the largest input using the RESIZE function.

Note: Functions will typically allow input values outside of the acceptable range to be passed but such values will return NaN in the results.

Examples

Cumulative

>> prob = expdf('c',[3.7942 4.6052],2)
prob =
    0.8500    0.9000
>> x = 0:0.1:8;
>> plot(x,expdf('c',x,2),'b',x,expdf('c',x,0.5),'r')

Density

>> prob = expdf('d',[3.7942 4.6052],2)
prob =
    0.0750    0.0500
>> x = 0:0.1:8;
>> plot(x,expdf('d',x,2),'b',x,expdf('d',x,0.5),'r')

Quantile

>> prob = expdf('q',[0.85 0.9],2)
prob =
     3.7942    4.6052

Random

>> prob = expdf('r',[4 1],2)
prob =
    0.3271
    2.3940
    0.9508
    3.9324

See Also

betadf, cauchydf, chidf, gammadf, gumbeldf, laplacedf, logisdf, lognormdf, normdf, paretodf, raydf, triangledf, unifdf, weibulldf