lognormdf Documentation


PLS_Toolbox Documentation: lognormdf	< logisdf	normdf >

lognormdf

Purpose

Lognormal distribution.

Synopsis

prob = lognormdf(function,x,a,b)

Description

Estimates cumulative distribution function (cumulative, cdf), probability density function (density, pdf), quantile (inverse of cdf), or random numbers for a Lognormal distribution.

This distribution may be used to characterize data that are themselves products or attribute data (square footage, acreage, etc.). The distribution is skewed to the right, but for very large means, may look nearly symmetric. Negative values in the sample are ignored.

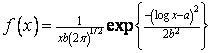
INPUTS:

function = [ {'cumulative'} | 'density' | 'quantile' | 'random' ], defines the functionality to be used. Note that the function recognizes the first letter of each string so that the string could be: [ 'c' | 'd' | 'q' | 'r' ].

x = matrix in which the sample data is stored, in the interval (-inf,inf).

for function=quantile - matrix with values in the interval (0,1).

for function=random - vector indicating the size of the random matrix to create.

a = mean parameter (real and positive).

b = standard deviation parameter (real and positive).

Note: If inputs (x, a, and b) are not equal in size, the function will attempt to resize all inputs to the largest input using the RESIZE function.

Note: Functions will typically allow input values outside of the acceptable range to be passed but such values will return NaN in the results.

Examples

Cumulative:

>> prob = lognormdf('c',0.99,1,2)

prob =

0.3068

>> x = [0:0.1:10];

>> plot(x,lognormdf('c',x,1,2),'b-',x,lognormdf('c',x,3,7),'r-')

Density:

>> prob = lognormdf('d',0.99,1,1)

prob =

0.2420

>> x = [0:0.1:10];

>> plot(x,lognormdf('d',x,2,1),'b-',x,lognormdf('d',x,0.5,1),'r-')

Quantile:

>> prob = lognormdf('q',0.99,0.5,1)

prob =

16.8837

Random:

>> prob = lognormdf('r',[4 1],2,1)

ans =

13.5191

4.4913

19.8518

8.7712