lmoptimizebnd
Purpose
Levenberg-Marquardt bounded non-linear optimization.
Synopsis
[x,fval,exitflag,out] =
lmoptimizebnd(fun,x0,xlow,xup,options,params)
Description
Starting at (x0)
LMOPTIMIZE finds (x) that minimizes the
function defined by the function handle (fun) where (x) has  parameters. Inputs (xlow) and (xup) can be used to provide
lower and upper bounds on the solution (x). The function (fun) must supply the Jacobian and Hessian i.e. they
are not estimated by LMOPTIMIZEBND
(an example description is provided in the Algorithm Section of the function LMOPTIMIZE).
parameters. Inputs (xlow) and (xup) can be used to provide
lower and upper bounds on the solution (x). The function (fun) must supply the Jacobian and Hessian i.e. they
are not estimated by LMOPTIMIZEBND
(an example description is provided in the Algorithm Section of the function LMOPTIMIZE).
INPUTS:
fun = function handle, the call to fun is
[fval,jacobian,hessian] = fun(x)
[see the Algorithm
section for tips on writing (fun)]
(fval) is a scalar objective function value,
(jacobian)
is a  x1
vector of Jacobian values, and
x1
vector of Jacobian values, and
(hessian) is a  x
x matrix of Hessian values.
matrix of Hessian values.
x0 =  x1 initial guess of the function
parameters.
x1 initial guess of the function
parameters.
xlow =  x1 vector of corresponding lower
bounds on (x). See options.alow. If an element
of xlow == -inf, the
corresponding parameter in (x)
is unbounded on the low side.
x1 vector of corresponding lower
bounds on (x). See options.alow. If an element
of xlow == -inf, the
corresponding parameter in (x)
is unbounded on the low side.
xup =  x1 vector of corresponding upper
bounds on (x). See options.aup. If an element
of xup == inf, the
corresponding parameter in (x)
is unbounded on the high side.
x1 vector of corresponding upper
bounds on (x). See options.aup. If an element
of xup == inf, the
corresponding parameter in (x)
is unbounded on the high side.
OPTIONAL INPUTS:
options = discussed below in the Options Section.
params = comma separated list of additional parameters passed
to the objective function (fun),
the call to (fun) is
[fval,jacobian,hessian] = fun(x,params1,params2,...).
OUTPUTS:
x =  x1 vector of parameter value(s) at
the function minimum.
x1 vector of parameter value(s) at
the function minimum.
fval = scalar value of the function evaluated at (x).
exitflag
= describes the exit condition with the following values
1: converged to a solution (x) based on one of the
tolerance criteria
0: convergence terminated based on maximum
iterations or maximum time.
out = structure array with the following fields:
critfinal: final
values of the stopping criteria (see options.stopcrit above).
x: intermediate values of (x) if options.x=='on'.
fval: intermeidate values of (fval) if options.fval=='on'.
Jacobian: last evaluation of the Jacobian if options.Jacobian=='on'.
Hessian: last evaluation of the Hessian if options.Hessian=='on'.
Algorithm
The algorithm is essentially the same as that discussed in LMOPTIMIZE and this section
discusses only the two main differences between LMOPTIMIZEBND and LMOPTIMIZE.
The first difference is the addition of penalty functions used
to enforce bounding. For example, the objective function used in LMOPTIMIZE is 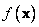 , but the
objective function used by LMOPTIMIZEBND
is
, but the
objective function used by LMOPTIMIZEBND
is 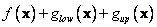 .
The penalty functions for upper,
.
The penalty functions for upper,  , and lower bounds,
, and lower bounds, 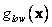 , are similar,
so only the lower penalty function is described.
, are similar,
so only the lower penalty function is described.
Define 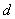 as the lower boundary,
as the lower boundary, 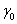 a small number
(e.g. 0.001) and
a small number
(e.g. 0.001) and 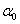 a large number [e.g.
a large number [e.g. 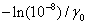 ], then for a
single parameter the lower penalty function is given as
], then for a
single parameter the lower penalty function is given as
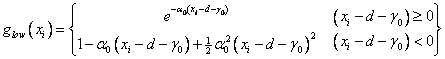 .
.
This function can be considered an external point function
because it is defined outside the feasible region (outside the boundaries). It
is continuous at the boundary and also has continuous first and second
derivatives. This is in contrast to internal point functions such as a log
function that is not continuous at the boundary [e.g. 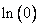 is not continuous]. The
first and second derivatives of the penalty function are given by
is not continuous]. The
first and second derivatives of the penalty function are given by
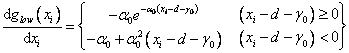 and
and
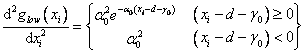 .
.
The external point penalty function does not guarantee that
a step won’t move outside the boundaries into the infeasible region. It does, however
provide a means for getting back inside the feasible region.
A second modification is included in the LMOPTIMIZEBND algorithm to
avoid large steps outside the feasible region. If a step 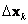 is such that any
is such that any  are outside the
feasible region, the step size for those parameters is reduced. The reduction
is 90% the distance of that parameter to the boundary. This typically changes
the direction of the step
are outside the
feasible region, the step size for those parameters is reduced. The reduction
is 90% the distance of that parameter to the boundary. This typically changes
the direction of the step 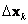 .
.
Options
options =
structure array with the following fields:
name: 'options', name indicating that this is an
options structure.
display: [
'off' | {'on'} ] governs level of
display to the command window.
dispfreq: N, displays results every Nth
iteration {default N=10}.
stopcrit: [1e-6 1e-6 10000 3600] defines the stopping criteria
as [(relative tolerance) (absolute tolerance) (maximum number of iterations)
(maximum time in seconds)].
x: [ {'off'} | 'on'
] saves (x) at each
step.
fval: [ {'off'} | 'on'
] saves (fval) at each
step.
Jacobian: [ {'off'}
| 'on' ] saves last
evaluation of the Jacobian.
Hessian: [ {'off'}
| 'on' ] saves last
evaluation of the Hessian.
ncond = 1e6, maximum condition number for the Hessian
(see Algorithm).
lamb = [0.01 0.7 1.5], 3-element vector used for damping
factor control (see Algorithm Section):
lamb(1): lamb(1)
times the biggest eigenvalue of the Hessian is added to Hessian eigenvalues
when taking the inverse; the result is damping.
lamb(2): lamb(1) = lamb(1)/lamb(2)
causes deceleration in line search.
lamb(3): lamb(1) = lamb(1)/lamb(3)
causes acceleration in line search.
ramb = [1e-4 0.5 1e-6], 3-element vector used to control the
line search (see Algorithm Section):
ramb(1): if fullstep < ramb(1)*[linear step] back
up (start line search).
ramb(2): if fullstep > ramb(2)*[linear step],
accelerate [change lamb(1)
by the acceleration parameter
lamb(3)].
ramb(3): if linesearch
rejected, make a small movement in direction of L-M step ramb(3)*[L-M step].
kmax = 50, maximum steps in line search (see Algorithm
Section).
alow: [ ],  x1 vector of penalty
weights for lower bound, {default = ones(N,1)}. If an element is zero, the corresponding parameter
in (x) is not bounded
on the low side.
x1 vector of penalty
weights for lower bound, {default = ones(N,1)}. If an element is zero, the corresponding parameter
in (x) is not bounded
on the low side.
aup: [ ],  x1 vector of penalty
weights for upper bound, {default = ones(N,1)}. If an element is zero, the corresponding parameter
in (x) is not bounded
on the high side.
x1 vector of penalty
weights for upper bound, {default = ones(N,1)}. If an element is zero, the corresponding parameter
in (x) is not bounded
on the high side.
Examples
options = lmoptimize('options');
options.x = 'on';
options.display = 'off';
options.alow = [0 0]; %x(1) and x(2) unbounded on low side
options.aup = [1 0]; %x(1) bounded on high side and x(2)
% unbounded on high side
[x,fval,exitflag,out] = lmoptimize(@banana,x0,[0 0], ...
[0.9
0],options);
plot(out.x(:,1),out.x(:,2),'-o','color', ...
[0.4 0.7 0.4],'markersize',2,'markerfacecolor', ...
[0 0.5 0],'markeredgecolor',[0
0.5 0])
See Also
function_handle, lmoptimize
![]() parameters. Inputs (xlow) and (xup) can be used to provide
lower and upper bounds on the solution (x). The function (fun) must supply the Jacobian and Hessian i.e. they
are not estimated by LMOPTIMIZEBND
(an example description is provided in the Algorithm Section of the function LMOPTIMIZE).
parameters. Inputs (xlow) and (xup) can be used to provide
lower and upper bounds on the solution (x). The function (fun) must supply the Jacobian and Hessian i.e. they
are not estimated by LMOPTIMIZEBND
(an example description is provided in the Algorithm Section of the function LMOPTIMIZE).![]() , but the
objective function used by LMOPTIMIZEBND
is
, but the
objective function used by LMOPTIMIZEBND
is ![]() .
The penalty functions for upper,
.
The penalty functions for upper, ![]() , and lower bounds,
, and lower bounds, ![]() , are similar,
so only the lower penalty function is described.
, are similar,
so only the lower penalty function is described.![]() as the lower boundary,
as the lower boundary, ![]() a small number
(e.g. 0.001) and
a small number
(e.g. 0.001) and ![]() a large number [e.g.
a large number [e.g. ![]() ], then for a
single parameter the lower penalty function is given as
], then for a
single parameter the lower penalty function is given as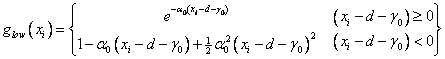 .
.![]() is not continuous]. The
first and second derivatives of the penalty function are given by
is not continuous]. The
first and second derivatives of the penalty function are given by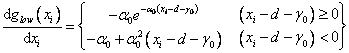 and
and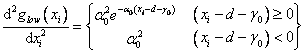 .
.![]() is such that any
is such that any ![]() are outside the
feasible region, the step size for those parameters is reduced. The reduction
is 90% the distance of that parameter to the boundary. This typically changes
the direction of the step
are outside the
feasible region, the step size for those parameters is reduced. The reduction
is 90% the distance of that parameter to the boundary. This typically changes
the direction of the step ![]() .
.