|
|
|
| PLS_Toolbox Documentation: lmoptimize | < leverag | lmoptimizebnd > |
lmoptimize
Purpose
Levenberg-Marquardt non-linear optimization.
Synopsis
[x,fval,exitflag,out] = lmoptimize(fun,x0,options,params)
Description
Starting at (x0)
LMOPTIMIZE finds (x) that minimizes the
function defined by the function handle (fun) where (x) has 
parameters. The function (fun) must supply the
Jacobian and Hessian i.e. they are not estimated by LMOPTIMIZE (an example is provided in the
Algorithm Section below).
INPUTS:
(jacobian)
is a x1
vector of Jacobian values, and
(hessian) is a x matrix of Hessian values.
x0 = x1 initial guess of the function
parameters.
OPTIONAL INPUTS:
OUTPUTS:
x = x1 vector of parameter value(s) at
the function minimum.
Algorithm
The objective function is defined as 
, where 
is a x1 vector. The
Jacobian 
and
the symmetric Hessian 
are defined as
.
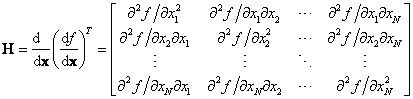Two types of calls to the function fun are made. The first type is used often and is a simple evaluation of the function at x given by
fval = fun(x,params1,params2,...);
The second type of call returns the Jacobian and Hessian
[fval,jacobian,hessian] = fun(x,params1,params2,...);
Therefore, to enhance the speed of the optimization, the M-file that evaluates the objective function should only evaluate the Jacobian and Hessian if nargout>1 as in the following example.
function [p,p1,p2] = banana(x)
%BANANA Rosenbrock's function
% INPUT:
% x = 2 element vector [x1 x2]
% OUTPUTS:
% p = P(x) = 100(x1^2-x2)^2 + (x1-1)^2
% p1 = P'(x) = [400(x1^3-x1x2) + 2(x1-1); -200(x1^2-x2)]
% p2 = P"(x) = [1200x1^2-400x2+2, -400x1; -400x1, 200]
% p is (fval)
% p1 is (jacobian)
% p2 is (Hessian)
%
%I/O: [p,p1,p2] = banana(x);
x12 = x(1)*x(1);
x13 = x(1)*x12;
x22 = x(2)*x(2);
alpha = 10; %1 is not very stiff, 10 is The stiff function
p = 10*alpha*(x13*x(1)-2*x12*x(2)+x22) + x12-2*x(1)+1;
if nargout>1
p1 = [40*alpha*(x13-x(1)*x(2)) + 2*(x(1)-1);
-20*alpha*(x12-x(2))];
p2 = [120*x12-40*x(2) + 2, -40*x(1);
-40*x(1), 20]*alpha;
end
This example shows that the Jacobian and Hessian are not
evaluated unless explicitly called for by utilizing the nargout command. Since estimating (output p1) and (output p2) can be time consuming,
this coding practice is expected to speed up the optimization.
A single step in a Gauss-Newton (G-N) optimization, 
is given as
where the index 
corresponds to the step number.
A problem with the G-N methods is that the inverse of the Hessian may not exist at every step, or it can converge to a saddle point if the Hessian is not positive definite [T.F. Edgar, D.M. Himmelblau, Optimization of Chemical Processes, 1st ed., McGraw-Hill Higher Education, New York, NY, 1988]. As an alternative, the Levenberg-Marquardt (L-M) method was used for CMF [K. Levenberg, Q. Appl. Math 2 (1944) 164; D. Marquardt, S.I.A.M. J. Appl. Math 11 (1963) 431; Edgar et al.]. A single step for the L-M method is given by
where 
is a damping parameter and 
is a x identity
matrix. This has a direct analogy to ridge regression [A.E. Hoerl, R.W. Kennard,
K.F. Baldwin, Commun. Statist. 4 (1975) 105] with , the ridge parameter,
constraining the size of the step. This method is also called a damped G-N
method [G. Tomasi, R. Bro, Comput. Stat. Data Anal. in press (2005)]. There
are several details to implementing the L-M approach [M. Lampton, Comput. Phys.
11 (1997) 110]. Details associated with the LMOPTIMIZE function are discussed here.
At each iteration in the algorithm, the inverse of 
must be estimated.
As a part of this process the singular value decomposition (SVD) of 
is calculated
as
.
Note that the left and right singular vectors are the same
(and equal to 
)
because the Hessian is symmetric. If the optimization surface is convex, will be
positive definite and the diagonal matrix 
will have all positive values on
the diagonal. However, the optimization problem may be such that this is not
the case at every step. Therefore a small number 
is added to the diagonal of in an effort to
ensure that the Hessian will always be positive definite. In the algorithm 
, where 
is the largest
singular value and 
is the maximum condition number
desired for the Hessian [ is input as options.ncond]. This can be
viewed as adding a small dampening to the optimization and is always included
at every step. In contrast, an additional damping factor that is allowed to
adapt at each step is also included. The adapting dampening factor is given by 
where the
initial 
is
input to the algorithm as options.lamb(1).
It is typical that is much larger than . The inverse
for the L-M step is then estimated as
and is used to estimate a step distance .
The ratio 
is a measure of the improvement in
the objective function relative to the improvement if the objective function
decreased linearly. If 
then a line search is initiated [
is a small
number input as options.ramb(1)].
In this case, the damping factor is increased (so that the step
size is reduced) by setting 
where 
[
is input as options.lamb(2)], and a new
step distance is
estimated. The ratio 
is then estimated again. The
damping factor is increased until 
or the maximum
number of line search steps 
is reached [ is input as options.kmax]. (If increases
sufficiently, the optimization resembles a damped steepest decent method.) If
the maximum number of line search steps is reached, the step is “rejected”
and only a small movement is made such that 
[
is input as options.ramb(3)].
If instead, the first estimate of the ratio is large enough
such that then
the line search is not initiated. If the ratio is sufficiently large such that 
, where 
then the
damping factor is decreased by setting 
where 
[
is input as options.ramb(2); 
is input as options.lamb(3)].
A new value for is then estimated from 
and the next
step is repeated from that point. The process is repeated until one of the
stopping criteria [options.stopcrit]
are met.
Options
Examples
options = lmoptimize('options');
options.x = 'on';
options.display = 'off';
[x,fval,exitflag,out] = lmoptimize(@banana,x0,options);
plot(out.x(:,1),out.x(:,2),'-o','color', ...
[0.4 0.7 0.4],'markersize',2,'markerfacecolor', ...
[0 0.5 0],'markeredgecolor',[0 0.5 0])
See Also
function_handle, lmoptimizebnd
| < leverag | lmoptimizebnd > |