alignmat Documentation


PLS_Toolbox Documentation: alignmat	< abline	als >

alignmat

Purpose

Alignment of matrices and N-way arrays

Synopsis

[bi,itst] = alignmat(amodel,b);

[bi,itst] = alignmat(a,b,nocomp);

Description

In some cases, data arrays require alignment to aid the performance of the three-way (e.g. GRAM, or PARAFAC) or unfold models such as MPCA. For example, sometimes GC peaks or data from batch operations can be shifted on a sample-to-sample basis (each sample is a M_b by N matrix). In these cases, it is advantageous to choose a sub-matrix of a single matrix A as a standard and find the sub-matrix of subsequent samples B that best align or match the standard matrix. It is also possible to use a model of one or more standard matrices A_model and find the sub-matrix of subsequent samples B that best align or match the model. In the latter case, it is also possible to find the sub-array of B that best aligns with the model of a N-way data set (A_model). This can be performed along multiple modes using ALIGNMAT.

ALIGNMAT finds the subarray of b, bi, that most matches a using two different algorithms. For input:

[bi,itst] = alignmat(amodel,b);

the sub-array bi is found using a projection method. In this case, bi is the sub-array of b that has the lowest residuals on a model of a called amodel. Models for amodel are standard model structures from PCA, PCR, GRAM, TLD, or PARAFAC. Input b can be class "double" or "dataset" and must have the same number of modes/dimensions as a with each element of size(b) ≥ size(a). Alignment is performed for modes with size(b) > size(a).

For input:

[bi,itst] = alignmat(a,b,ncomp);

both a and b can be class "double" or "dataset", but both are two-way arrays (matrices). For a M by N then b must be Mb by N where Mb ≥ M (when Mb = M no alignment is performed). The output bi is the sub-array of b that best matches the matrix a. Optional input ncomp is a scalar of the number of components to use in the decomposition {default: ncomp = 1}.

Output bi is an array of class "double", itst is a cell array containing the indices of b that match bi. Note that since interpolation is used the indices in itst are not in general integers.

Algorithm

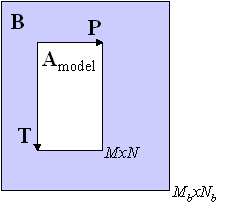For the projection method, A_model is a model of array A. This can be a model from PCA, GRAM, TLD, or PARAFAC. For example, if A is a M by N matrix then the PCA model of A is where T is M by K and P is N by K. Alignmat finds the submatrix of B, B_i, that has the lowest residuals on the model of A i.e. . This can be used to find the data “cube” within N-way arrays.

In the figure, this is represented as having each of the M by N sub-matrices of B projected onto the model of the M by N model of A. Note that in the figure that the size of B is M_b by N_b with M_b>M and N_b>N.

The projection method was presented in Gallagher, N.B. and Wise, B.M., “Standardization for Three-Way Analysis”, TRICAP 2000: Three-way Methods in Chemistry and Psychology, Hvedholm Castle, Faaborg, Denmark, July (2000). In that study, it was found that the projection method was faster and more robust than the SVD-based algorithm discussed below.

In the SVD method, the standard matrix A and a sub-matrix of B, B_i, are aumented and a singular value decomposition of the result is performed such that [u,s,v] = svd([A_MxN|B_iMxNb]). The sub-matrix is incremented and the SVD is performed again. The sub-matrix that minimizes the rank is selected as matching best. The objective function is 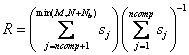. Note that in this algorithm N and N_b do not have to be equal. The algorithm is discussed in Prazen, et al., Anal. Chem., 70, 218-225, 1998.