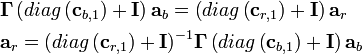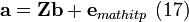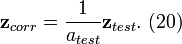Oplecorr
Contents |
Purpose
Optical path-length estimation and correction with closure constraints.
Synopsis
- model = oplecorr(x,y,ncomp,options); %identifies model (calibration)
- sx = oplecorr(x,model,options); %applies the model
Description
The OPLEC model is similar to EMSC but doesn't require esimates of the pure spectra for filtering. Instead it assumes closure on the chemical analyte contributions and the use of a non-chemical signal basis P defined by the input (options.order). For example, if options.order = 2, then P = [1, (1:n)', (1:n)'.^2] to account for offset, slope and curvature in the baseline.
Inputs
- x = X-block (2-way array class "double" or "dataset"), and
- ncomp = number of components to to be calculated (positive integer scalar).
1) Calibration: model = oplecorr(x,y,ncomp,options);
- x = M by N matrix of spectra (class "double" or "dataset").
- y = M by 1 matrix of known reference values.
- ncomp = number of components to to be used for the basis Z (positive integer scalar).
- options = an optional input structure array described below.
2) Apply: sx = oplecorr(x,model,options);
- x =M by N matrix of spectra to be correctected .
- model = oplecorr model.
Outputs
- model = oplecorr model is a model structure with the following fields (see Standard Model Structure for additional information):
- modeltype: 'OPLECORR',
- datasource: structure array with information about input data,
- date: date of creation,
- time: time of creation, ...
- and
- sx = a M by N matrix of filtered ("corrected") spectra.
Options
options = a structure array with the following fields:
- display: [ {'off'}| 'on' ] governs level of display to the command window.
- order: defines the order of polynomial to describe 'non-chemical' signal due to physical artifacts.
- Alternatively, (order) can be a N by Kp matrix corresponding to basis vectors to account for non-chemical signal.
- This portion of the signal is not included in the closure constraint. See Algorithm for a more complete description.
- center: [ {false} | true] governs mean-centering of the PLS model that regresses the corrections factors (model.b). No centering (the default) results in a force fit through zero.
Algorithm
The OPLEC algorithm is based on the work Z-P Chen, J Morris, E Martin, “Extracting Chemical Information from Spectral Data with Multiplicative Light Scattering Effects by Optical Path-Length Estimation and Correction,” Anal. Chem., 78, 7674-7681 (2006). OPLEC is similar to extended multiplicative scatter correction (EMSC) except that it incorporates closure in the signal due to chemical analytes.
It is assumed that the measured signal, 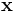 can be modeled as
can be modeled as
where 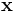 is a
is a 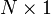 column vector,
column vector, 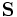 is a
is a 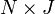 matrix with columns corresponding to analyte spectra,
matrix with columns corresponding to analyte spectra, 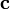 is a
is a 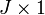 vector of contributions,
vector of contributions, 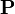 is a matrix with columns corresponding to physical artifacts in the spectra and
is a matrix with columns corresponding to physical artifacts in the spectra and 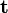 is a vector corresponding scores (or contributions for the artifacts). The factor
is a vector corresponding scores (or contributions for the artifacts). The factor  is a multiplicative factor (e.g. due to changes in path-length) identified by the OPLEC algorithm. The
is a multiplicative factor (e.g. due to changes in path-length) identified by the OPLEC algorithm. The 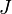 analyte contributions are subject to closure such that
analyte contributions are subject to closure such that
Closure also implies that the contributions are non-negative. It is assumed that the contributions to the first analyte are known (i.e., the 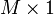 column vector
column vector 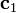 is known). It is also assumed that the matrix
is known). It is also assumed that the matrix 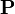 can be modeled a priori. Examples for physical artifacts include an offset, slope and curvature of the baseline that can be accounted for by the
can be modeled a priori. Examples for physical artifacts include an offset, slope and curvature of the baseline that can be accounted for by the 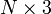 basis
basis
where 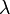 is the wavelength (or frequency) axis. However, it should be clear that
is the wavelength (or frequency) axis. However, it should be clear that 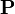 is a matrix with columns that span physical artifacts not subject to closure. The
is a matrix with columns that span physical artifacts not subject to closure. The 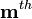 measured signal,
measured signal, 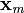 ,
, 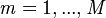 , orthogonal to
, orthogonal to 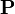 is
is
where 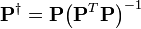 ,
, 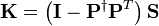 , and
, and 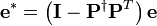 .
The measurements can be collected into a matrix
.
The measurements can be collected into a matrix 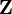 and it is recognized that a basis for the
and it is recognized that a basis for the 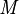 measurements,
measurements, 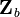 , can be obtained from a subset of linearly independent measurements. Partitioning
, can be obtained from a subset of linearly independent measurements. Partitioning 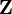 into the basis and remaining measurements,
into the basis and remaining measurements, 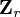 , gives
, gives
This partitioning implies that the remaining measurements, 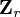 , are linear combinations of
, are linear combinations of 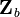 such that
such that
where
Expanding a single measurement in 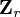 gives
gives
Substitution of Equation (2) into (8) gives
where 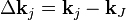 .
The partitioned matrices in Equation (5) can now be written using the last expression of Equation (9) to give
.
The partitioned matrices in Equation (5) can now be written using the last expression of Equation (9) to give
Noting the relationship in Equation (6) gives
Equating terms in Equation (11) gives two additional relationships:
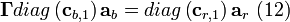 , and
, and
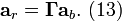
Substitution of Equation (13) into (12) gives
Recall that 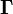 ,
, 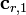 and
and 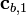 are known but
are known but 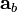 is unknown. However, as with MSC where the reference used for correction is arbitrary (e.g., the mean of the calibration set is often used as the spectrum to “correct to”), any element of
is unknown. However, as with MSC where the reference used for correction is arbitrary (e.g., the mean of the calibration set is often used as the spectrum to “correct to”), any element of 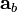 can be set to one. Setting the first element of
can be set to one. Setting the first element of 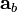 to one and rearranging Equation (14) yields
to one and rearranging Equation (14) yields
Recognizing that the corrections, 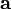 , must be non-negative implies that the remaining correction factors
, must be non-negative implies that the remaining correction factors 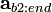 should be obtained by solving Equation (15) using non-negative least squares. The result is correction factors for all the basis vectors
should be obtained by solving Equation (15) using non-negative least squares. The result is correction factors for all the basis vectors
![\mathbf{a}_{b}^{T}=\left[ \begin{matrix}
1 & \mathbf{a}_{b,\left( 2:end \right)}^{T} \\
\end{matrix} \right]](math_2bce.png) . that can be substituted into the sum of Equations (12) to give
. that can be substituted into the sum of Equations (12) to give
The correction factors can be collected into a single vector given by
![{{\mathbf{a}}^{T}}=\left[ \begin{matrix}
\mathbf{a}_{b}^{T} & \mathbf{a}_{r}^{T} \\
\end{matrix} \right]\text{ (16)}](math_7790.png) .
.
Next, a regression model is obtained to allow estimation of correction factors for future test samples using the following
where the regression vector, 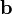 , is estimated using PLS. Change options.center to true to use mean-centering for the PLS model. The correction factors for test samples are calculated using the following steps
, is estimated using PLS. Change options.center to true to use mean-centering for the PLS model. The correction factors for test samples are calculated using the following steps
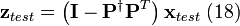 , and
, and
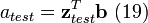
where the corrected spectrum is then given by
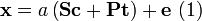
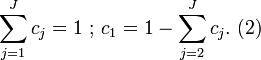
![\mathbf{P}=\left[ \begin{matrix}
\mathbf{1} & \lambda & {{\lambda }^{2}} \\
\end{matrix} \right]\text{ (3)}](math_7a56.png)
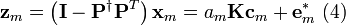
![\mathbf{Z}=\left[ \begin{matrix}
{{\mathbf{Z}}_{b}} \\
{{\mathbf{Z}}_{r}} \\
\end{matrix} \right]=\left[ \begin{matrix}
diag\left( {{\mathbf{a}}_{b}} \right){{\mathbf{C}}_{b}}{{\mathbf{K}}^{T}} \\
diag\left( {{\mathbf{a}}_{r}} \right){{\mathbf{C}}_{r}}{{\mathbf{K}}^{T}} \\
\end{matrix} \right]+{{\mathbf{E}}^{*}}\text{ (5)}](math_e7ab.png)
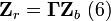
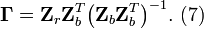
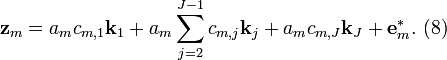
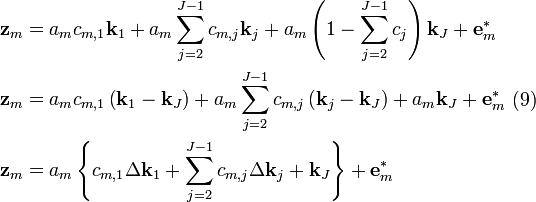
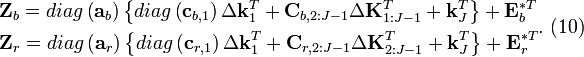
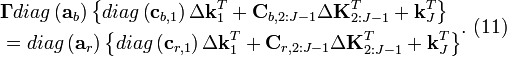
![\begin{align}
& \mathbf{\Gamma} diag\left( {{\mathbf{c}}_{b,1}} \right){{\mathbf{a}}_{b}}=diag\left( {{\mathbf{c}}_{r,1}} \right)\mathbf{\Gamma} {{\mathbf{a}}_{b}} \\
& {{\left[ \mathbf{\Gamma} \odot \left( \mathbf{1c}_{b,1}^{T} \right) \right]}_{{{M}_{r}}\times J}}{{\left( {{\mathbf{a}}_{b}} \right)}_{J\times 1}}={{\left[ \left( {{\mathbf{c}}_{r,1}}{{\mathbf{1}}^{T}} \right)\odot \Gamma \right]}_{{{M}_{r}}\times J}}{{\left( {{\mathbf{a}}_{b}} \right)}_{J\times 1}} \\
\end{align}.\text{ (14)}](math_8c55.png)
![\begin{align} & {{c}_{b,\left( 1,1 \right)}}{{\mathbf{\Gamma} }_{:,1}}+\left[ {{\mathbf{\Gamma} }_{:,2:J}}\odot \left( \mathbf{1c}_{b,\left( 2:J,1 \right)}^{T} \right) \right]{{\mathbf{a}}_{b,\left( 2:end,2 \right)}}={{\mathbf{c}}_{r,\left( :,1 \right)}}\odot {{\mathbf{\Gamma} }_{:,1}}+\left[ \left( {{\mathbf{c}}_{r,\left( :,1 \right)}}{{\mathbf{1}}^{T}} \right)\odot {{\mathbf{\Gamma} }_{:,2:J}} \right]{{\mathbf{a}}_{b,\left( 2:end,2 \right)}} \\
& \left[ {{\mathbf{\Gamma} }_{:,2:J}}\odot \left( \mathbf{1c}_{b,\left( 2:J,1 \right)}^{T} \right)-\left( {{\mathbf{c}}_{r,\left( :,1 \right)}}{{\mathbf{1}}^{T}} \right)\odot {{\mathbf{\Gamma} }_{:,2:J}} \right]{{\mathbf{a}}_{b,\left( 2:end,2 \right)}}=\left( {{\mathbf{c}}_{r,\left( :,1 \right)}}-\mathbf{1}{{c}_{b,\left( 1,1 \right)}} \right)\odot {{\mathbf{\Gamma} }_{:,1}} \\
\end{align}.\text{ (15)}](math_5c81.png)