Line filter

Line filter

Purpose

Spectral filtering via convolution and deconvolution.

Synopsis

xf = line_filter(x,win,options);

Description

Inputs

• x = MxN matrix of data of class 'double' or 'dataset'. If 'dataset' it must x.type=='data'. Each of the M rows are convolved with the linear filter given in (options.lineshape).
• win =

1) A scalar parameter corresponding to the analogous window width of the filter.

options.psf =

'gaussian', (win) corresponds to the std in the Gaussian distribution.

'box', (win) is the half-width in number of channels.

'triangular', (win) is the half-width in channels.

2) If (win) is 1xN vector, then it is used as the PSF and (options.psf) is ignored. The FFT of the PSF is calculated and used in the convolution or deconvolution algorithm.

Outputs

• xf = Filtered data of class 'dataset'.

Options

options = a structure array with the following fields:

• psf: [ {'gaussian'} | 'box' | 'triangular'] Line shape or point source function (PSF) for filtering.
• conv: [ {'convolve'} | 'deconvolve' ] Governs the algorithm and tells it to convolve with the point source function given in (options.psf) or deconvolve. If 'deconvolve', then (options.reg) is used.
• reg: {1e-6} regularization parameter (this parameter is used for ridging in the deconvolution algorithm).

Algorithm

If options.conv = 'convolve' {the default}, then convolution is performed. The inputs are 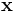$\mathbf{x}$, a 1xN vector containing the signal, and 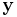$\mathbf{y}$ a 1xN vector containing a point source function. Then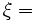 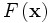$\mathbf{\xi } =$ $F\left( \mathbf{x} \right)$ is the FFT of the signal and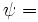 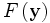$\mathbf{\psi } =$ $F\left( \mathbf{y} \right)$ are the corresponding Fourier transforms. The convolved signal is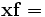 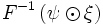$\mathbf{xf } =$ $F^{-1} \left( \mathbf{\psi} \odot \mathbf{\xi} \right)$ where $\odot$ is the element-by-element Hadamard product.

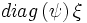If options.conv = 'deconvolve', then deconvolution is performed. 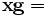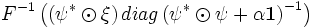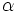Noting that $\mathbf{\psi} \odot \mathbf{\xi}$ can be written as $diag \left( \mathbf{\psi} \right) \mathbf{\xi}$, the deconvolved signal is given as $\mathbf{xg } =$ $F^{-1} \left( \left( \mathbf{\psi}^{*} \odot \mathbf{\xi} \right) diag \left( \mathbf{\psi}^{*} \odot \mathbf{\psi} + \alpha\mathbf{1} \right) ^{-1} \right)$ where $\alpha$ is the regularization parameter given in (options.reg) , 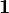$\mathbf{1}$ is a 1xN vector of ones and 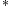$^{*}$ incicates complex conjugate.

See Also

savgol