Advanced Preprocessing: Multivariate Filtering
From Eigenvector Documentation Wiki
Contents |
Introduction
In some cases, there is insufficient selectivity in the variables to easily remove things like backgrounds or other signals which are interferences to a multivariate model. In these cases, using multivariate filtering methods before model calibration may help simplify the end model. Multivariate filters identify some unwanted covariance structure (i.e., how variables change together) and remove these sources of variance from the data prior to calibration or prediction. In a simple way, these filters can be viewed as pattern filters in that they remove certain patterns among the variables. The resulting data contain only those covariance patterns which passed through the filter and are, ideally, useful or interesting in the context of the model.
Identification of the patterns to filter can be based on a number of different criteria. The full discussion of multivariate filtering methods is outside the scope of this chapter, but it is worth noting that these methods can be very powerful for calibration transfer and instrument standardization problems, as well as for filtering out other differences between measurements which should otherwise be the same (e.g., differences in the same sample due to changes with time, or differences within a class of items being used in a classification problem).
One common method to identify the multivariate filter "target" uses the Y-block of a multivariate regression problem. This Y-block contains the quantitative (or qualitative) values for each sample and, theoretically, samples with the same value in the Y-block should have the same covariance structure (i.e., they should be similar in a multivariate fashion). A multivariate filter can be created which attempts to remove differences between samples with similar y-values. This filter should reduce the complexity of any regression model needed to predict these data. Put in mathematical terms, the multivariate filter removes signals in the X-block (measured responses) which are orthogonal to the Y-block (property of interest).
Three multivariate filtering methods are provided in the Preprocessing window: Orthogonal Signal Correction (OSC), Generalized Least Squares Weighting (GLSW), and External Parameter Orthogonalization (EPO) where this last one also encompasses Extended Mixture Model (EMM) filtering. In the context of the Preprocessing window, both methods require a Y-block and are thus only relevant in the context of regression models. Additionally, as of the current version of PLS_Toolbox, the graphical interface access to these functions only permits their use to orthogonalize to a Y-block, not for calibration transfer applications. From the command line, however, both of these functions can also be used for calibration transfer or other filtering tasks. For more information on these uses, please see the calibration transfer and instrument standardization chapter of this manual.
OSC (Orthogonal Signal Correction)
Orthogonal Signal Correction (Sjöblom et al., 1998) removes variance in the X-block which is orthogonal to the Y-block. Such variance is identified as some number of factors (described as components) of the X-block which have been made orthogonal to the Y-block. When applying this preprocessing to new data, the same directions are removed from the new data prior to applying the model.
The algorithm starts by identifying the first principal component (PC) of the X-block. Next, the loading is rotated to make the scores be orthogonal to the Y-block. This loading represents a feature which is not influenced by changes in the property of interest described in the Y-block. Once the rotation is complete, a PLS model is created which can predict these orthogonal scores from the X-block. The number of components in the PLS model is adjusted to achieve a given level of captured variance for the orthogonal scores. Finally, the weights, loadings, and predicted scores are used to remove the given orthogonal component, and are also set aside for use when applying OSC to a new unknown sample. This entire process can then be repeated on the "deflated" X-block (the X-block with the previously-identified orthogonal component removed) for any given number of components. Each cycle results in additional PLS weights and loadings being added to the total that will be used when applying to new data.
There are three settings for the OSC preprocessing method: number of components, number of iterations, and tolerance level. The number of components defines how many times the entire process will be performed. The number of iterations defines how many cycles will be used to rotate the initial PC loading to be as orthogonal to Y as possible. The tolerance level defines the percent variance that must be captured by the PLS model(s) of the orthogonalized scores.
In the Preprocessing window, this method allows for adjustment of the settings identified above. From the command line, this method is performed using the osccalc and oscapp functions.
GLS Weighting and EPO
Generalized Least Squares Weighting (GLSW) is a filter calculated from the differences between samples which should otherwise be similar. These differences are considered interferences or "clutter" and the filter attempts to down-weight (shrink) those interferences. A simplified version of GLSW is called External Parameter Orthogonalization (EPO), which does an orthogonalization (complete subtraction) of some number of significant patterns identified as clutter. A simplified version of EPO emulates the Extended Mixture Model (EMM) in which all identified clutter patterns are orthogonalized to.
Clutter Identification
In the case of a classification problem, similar samples would be the members of a given class. Any variation within each class group (known as "within-class variance") can be considered clutter which will make the classification task harder. The goal of GLSW in this case is to remove this within-class variance as much as possible without making the classes closer together (between-class variance).
In the case of a calibration transfer problem, similar samples would be data from the same samples measured on two different instruments or on the same instrument at two different points in time. The goal of GLSW is to down-weight the differences between the two instruments and, therefore, make them appear more similar. A regression model built from GLSW-filtered data can be used on either instrument after applying the filtering to any measured spectrum. Although this specific application of GLSW is not covered by this chapter, the description below gives the mathematical basis of this use.
GLSW can also be used prior to building a regression model in order to remove variance from the X-block which is mostly orthogonal to the Y-block. This application of GLSW is similar to OSC (see above), and such filtering can allow a regression model to achieve a required error of calibration and prediction using fewer latent variables. In this context, GLSW uses samples with similar Y-block values to identify the sources of variance to down-weight.
In all cases, the default algorithm for GLSW uses a single adjustable parameter, α, which defines how strongly GLSW downweights interferences. Adjusting α towards larger values (typically above 0.001) decreases the effect of the filter. Smaller αs (typically 0.001 and below) apply more filtering.
GLSW Algorithm
The GLSW algorithm will be described here for the calibration transfer application (because it is simpler to visualize) and then the use of GLSW in classification and regression applications will be described. In all cases, the approach involves the calculation of a covariance matrix from the differences between similar samples. In the case of calibration transfer problems, this difference is defined as the numerical difference between the two groups of mean-centered transfer samples. Given two sample matrices, X1 and X2, the data are mean-centered and the difference calculated:
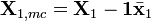 (1)
(1)
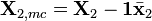 (2)
(2)
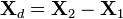 (3)
(3)
where 1 is a vector of ones equal in length to the number of rows in X1, 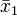 is the mean of all rows of X1, and
is the mean of all rows of X1, and 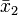 is the mean of all rows of X2. Note that this requires that X1 and X2 are arranged such that the rows are in the same order in terms of samples measured on the two instruments.
is the mean of all rows of X2. Note that this requires that X1 and X2 are arranged such that the rows are in the same order in terms of samples measured on the two instruments.
The next step is to calculate the covariance matrix, C:
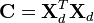 (4)
(4)
followed by the singular-value decomposition of the matrix, which produces the left eigenvectors, V, and the diagonal matrix of singular values, S:
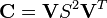 (5)
(5)
Next, a weighted, ridged version of the singular values is calculated
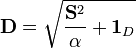 (6)
(6)
where 1D is a diagonal matrix of ones of appropriate size and α is the weighting parameter mentioned earlier. The scale of the weighting parameter depends on the scale of the variance in Xd. Finally, the inverse of these weighted eigenvalues are used to calculate the filtering matrix.
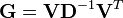 (7)
(7)
This multivariate filtering matrix can be used by simply projecting a sample into the matrix. The result of this projection is that correlations present in the original covariance matrix are down-weighted (to the extent defined by α ). The filtering matrix is used both on the original calibration data prior to model calibration, and any future new data prior to application of the regression model.
The choice of α depends on the scale of the original values but also how similar the interferences are to the net analyte signal. If the interferences are similar to the variance necessary to the analytical measurement, then α will need to be higher in order to keep from removing analytically useful variance. However, a higher α will decrease the extent to which interferences are down-weighted. In practice, values between 1 and 0.0001 are often used.
Y-Gradient GLSW
When using GLSW to filter out X-block variance which is orthogonal to a Y-block, a different approach is used to calculate the difference matrix, Xd . In this situation we have only one X-block, X, of measured calibration samples, but we also have a Y-block, y (here defined only for a single column-vector), of reference measurements. To a first approximation, the Y-block can be considered a description of the similarity between samples. Samples with similar y values should have similar values in the X-block.
In order to identify the differences between samples with similar y values, the rows of the X- and Y-blocks are first sorted in order of increasing y value. This puts samples with similar values near each other in the matrix. Next, the difference between proximate samples is determined by calculating the derivative of each column of the X-block. These derivatives are calculated using a 5-point, first-order, Savitzky-Golay first derivative (note that a first-order polynomial derivative is essentially a block-average derivative including smoothing and derivatizing simultaneously). This derivative yields a matrix, Xd , in which each sample (row) is an average of the difference between it and the four samples most similar to it. A similar derivative is calculated for the sorted Y-block, yielding vector yd , a measure of how different the y values are for each group of 5 samples.
At this point, Xd could be used in equation 4 to calculate the covariance matrix of differences. However, some of the calculated differences (rows) may have been done on groups of samples with significantly different y values. These rows contain features which are correlated to the Y-block and should not be removed by GLS. To avoid this, the individual rows of Xd need to be re-weighted by converting the sorted Y-block differences into a diagonal re-weighting matrix, W , in which the ith diagonal element, wi, is calculated from the rearranged equation
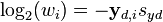 (8)
(8)
The value 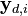 is the ith element of the yd vector, and syd is the standard deviation of y-value differences:
is the ith element of the yd vector, and syd is the standard deviation of y-value differences:
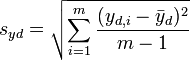 (9)
(9)
The re-weighting matrix is then used along with Xd to form the covariance matrix
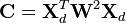 (10)
(10)
which is then used in equations 5 through 7 as described above.
External Parameter Orthogonalization (EPO)
An alternative multivariate filter called External Parameter Orthogonalization (EPO) uses the same process as GLSW except that only a certnain number of eigenvectors calculated in equation 5 are kept and the D matrix calculated in equation 6 is a diagonal vector of ones. The result is that X is "hard-orthogonalized" to the eigenvectors (the directions are completely removed) rather than simply "shrinking" these directions as is done with GLSW.
If all of the calculated eigenvectors are used in an EPO filter, the method becomes equivalent to the Extended Mixture Model (EMM) method described in Martens and Naes 1989.
For a literature reference on EPO, see: Roger, Chauchard, Bellon-Maurel, "EPO–PLS external parameter orthogonalisation of PLS application to temperature-independent measurement of sugar content of intact fruits." Chemom. Intell. Lab. Syst., 66, 191– 204 (2003).
Settings and Command-line Usage
In the Preprocessing window, the GLSW method has a Settings Window to allow for adjustment of the weighting parameter, α, whether or not to include mean-centering ("ignore means"), whether to use EPO mode and select a given number of components to orthongonalize to, or whether to use EMM/ELS mode in which the data is orthogonalized to all available components. From the command line, this method is performed using the glsw function, which also permits a number of other modes of application (including identification of "classes" of similar samples).